ActiveRecod如何拼出一句Sql?—— (零)刚好够用的关系代数基础
前言
还记得初次接触Rails,在controller里使用Post.all从数据库里拉出一张表的数据出来时,那种惊叹和感动吗?
如果你曾经写过DAO层,就知道ActiveRecord的实现是多么优雅。作为web最强框架,Rails提供了太多魔法一般的东西,Web App开发者能号称使用Rails 15分钟构建博客,是因为我们站在Rails厚重的一层封装上。任何优雅而便捷的框架背后都包含大量的技术含量。今天我们从ActiveRecord说起。
ActiveRecord是Rails里MVC的M层,本系列文章只选择其一个侧面介绍 – 调用Arel生成Sql语句。 Arel是一个SQL AST manager,ActiveRecord完全委托Arel管理Sql的生成,所以这个系列的标题,也可以说成是“ActiveRecord如何使用Arel拼出Sql?”。本系列假设你已对rails有一定了解,对sql有一定了解。
Arel的github主页的描述是:A Relational Algebra,关系代数(Relational Algebra)是Arel的理论基础。要明白Arel是如何工作的,必须要了解基本的关系代数知识,如果你对此已经了解,可以跳过本文。
关系代数(Relational algebra)
介绍关系代数之前,可以从远一点说起。在浏览器的控制台输入:
console.log(1 + 1);
在机器执行这句js语句时,需要把它编译成机器码。而在此过程中,需要得到一棵形如这样的AST:
在生成这棵语法树的过程中,计算机理论需要借助别的学科(主要是数学,语言学)的理论成果,如:自动状态机和上下文无关文法。
而关系代数和SQL的关系正是与之类似的:正如计算机编译器使用自动状态机和上下文无关语法作为理论武器,关系型数据库使用关系代数,规定了我们能对数据库中的表和数据做何种操作,获得哪些结果。(再复杂的Sql查询,都是通过几种关系运算叠加而来的。)
明白了关系代数的位置,再给出它的定义:
关系代数和普通代数(1 + 1 = 2)类似,只不过操作数和返回结果都是关系。(关系 + 关系 = 关系)
在我们的语境中,可以将关系粗暴的理解为表和表中的记录。
关系运算符
首先说说关系代数的运算规则。
基本的集合运算
关系代数中,关系可被看作集合,所以可以使用基本的集合运算:
- 交集(Union)
- 并集(Intersection)
- 差集(Different)
- 笛卡尔积(Cartesian product)
基本的集合运算比较简单,和普通的集合运算无异,在此不需赘述。值得注意的是,关系代数中,关系是有schema的,所以前三种运算(交、并、差)要求两个关系之间必须有相同的表结构。
专门的关系运算
专门的关系运算包括:
- 投影(Projection)
- 选择(Selection)
- 连接(Join)
这些运算就是Sql语句里代表的含义(select,where,join等),如果你对数据库,Sql有一定了解,这部分内容理解起来是很容易的。
我会以一张表的操作作为例子。先引入这样一张表:
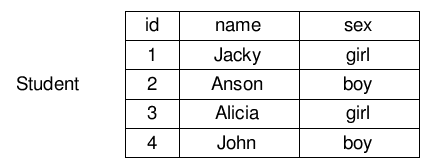
投影(Projection)(π)
关系R上的投影是从R中选择出若干属性列组成新的关系:
\[\pi_A(R) = \{ t[A] | t\in R \}\]以students表为例:当需要查找id,name字段时,sql语句将会是这样:
select id, name from students;
而用关系运算符表示的话,将会是这样:
\[\pi_{id,name}(students)\]运算结果是:
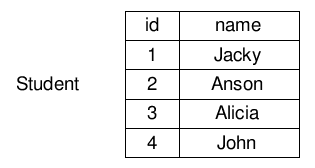
选择(Selection)(σ)
选择是在关系R中选择满足给定条件的诸元组,记作:
\[\sigma_F(R) = \{ t | t\in R \land F(t) = true\}\]还是以students表为例,当需要查找所有男生时,sql语句将会是这样:
select * from students where sex = 'boy';
而用关系运算符表示的话,将会是这样:
\[\sigma_{sex = boy}(students)\]运算结果是:
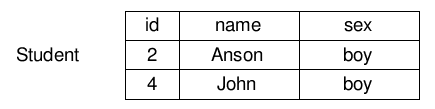
多次关系运算
关系运算符可以多次应用,一次查询可能是多次关系运算的结果,如:要查询所有男生的名字,sql语句是:
select name from students where sex = 'boy';
而用关系运算符翻译这句sql的话,将会是这样:
\[\pi_{name}(\sigma_{sex = boy}(students))\]运算过程和普通代数是一样的,像这样:
-
运算Selection的部分:
\[students := \sigma_{sex = boy}(students)\]得到的结果即为一个两行三列的关系。
-
对第一步的结果进行Projection运算:
\[students := \pi_{name}(students)\]得到最终两行一列的结果:
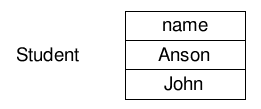
连接(Join)(⋈)
选择(Selection)和投影(Projection)都是一目运算符,而连接是二目运算符。再引入一个表:
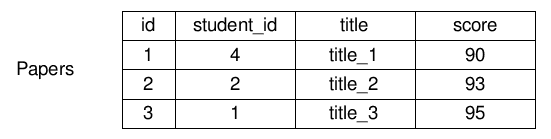
要查询看每个学生的论文,sql将会是:
select name, paper from students, papers where students.id = papers.student_id;
如果用关系运算符表示的话,会是这样:
\[\pi_{name,paper}(students \bowtie_{students.id = papers.student_id} papers)\]你可能已经想到,这表达式也可以不使用⋈运算符,它与这个(使用笛卡尔积的)表达式是等价的:
\[\pi_{name,paper}(\sigma_{students.id = papers.student_id}(students \times papers))\]关系运算中还有其他的一些运算符,如:重命名(Rename)(ρ),半联结(Semijoin) (⋉ / ⋊)等,这里不一一详细描述,如果想了解的话,请翻墙看各种资料。
关系运算符与树
当我们了解如何将Sql转换为关系运算时,会发现一个关系运算式很适合以树状结构表示,比如上面连接例子中的表达式:
\[\pi_{name,paper}(students \bowtie_{students.id = papers.student_id} papers)\]如果表示为树状结构,会是这样:
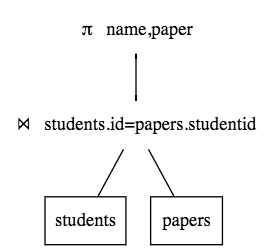
为什么这样的表达树比一句Sql语句更有价值呢?因为Sql语句描述的是做什么(what),而关系运算描述的是怎么做(how),有了这样的表达树,很容易使用一些算法技术进行分析操作。
实际上,数据库执行任何Sql的时候,的确会将sql语句转换为类似的AST。
Arel和关系运算
在文章的开头已经介绍了Arel和relational algebra的关系。在了解了后者之后,再去看Arel的源代码,才能明白它的设计思路和实现思路,和运行时的内存结构。
实际上,Arel生成Sql的步骤就是上文中将sql转换为关系运算表达式的 逆过程:
- Arel的运行时内存,持有一棵语法树 – 可以认为是关系运算表达式的树状形式。
- 另一些类,通过观察这棵语法树,拼出Sql语句。
当你看不明白Arel在相关部分的实现时,请多想想relational algebra的内容。
有了刚好够用的基础,接下来我们继续探讨ActiveRecord,Arel的源代码。
